
Exercícios de raciocínio lógico merecem bastante atenção na prova de Matemática e Suas Tecnologias no Enem.
Normalmente, são exercícios simples e fáceis que, devido à maneira de calcular a nota do Enem (TRI - Teoria de Resposta ao Item), podem render bons resultados para os candidatos que acertam esses exercícios.
Aprender dicas para resolver problemas lógicos é uma ótima forma de conquistar uma boa pontuação não só no Enem, mas em demais vestibulares e concursos públicos.
Alguns estudantes podem cair na cilada de pensar que, para responder perguntas de Matemática no Enem, é necessário aprender somente a “regra de três”, ou que perguntas de lógica são simples e podem ser resolvidas com um simples raciocínio.
Contudo, a verdade é que é preciso saber o que e como estudar.
A boa notícia é que você pode aprender dicas para solucionar questões de lógica no Enem. Como dissemos ali no início do texto, entender uma matéria que mistura filosofia e matemática pode soar confuso no início. Mas fique tranquilo!
A seguir, você vai aprender o que é o raciocínio lógico e também quais as melhores maneiras de resolver esses problemas na sua prova do Enem.
Confira:
A lógica na Filosofia é baseada na teoria do silogismo, criada por Aristóteles. Nessa teoria, o raciocínio é baseado na dedução. Para isso, duas proposições se conectam de tal forma que é possível deduzir uma terceira proposição, ou seja, a conclusão.
Já a lógica matemática se resume em determinar se uma proposição é verdadeira a partir do conteúdo dessa mesma proposição. Vamos explicar melhor essa parte mais à frente no texto.
Como mostramos, desde a Antiguidade a humanidade utiliza a lógica para entender conceitos e desenvolver novos teoremas.
O que você precisa entender agora é que, na Matemática, um teorema é uma afirmação (ou dedução) que pode ser provada por meio de outras deduções. Essas afirmações precisam já ter sido provadas como reais, com base em axiomas.
Os axiomas são verdades universais inquestionáveis. São usadas como base na construção de novos teoremas, como explicamos acima.
Em resumo, o teorema é a ampliação de conceitos matemáticos considerados inquestionáveis.
A lógica procura lidar com verdades universais incontestáveis e é indispensável para a Matemática. Seu objetivo é chegar a conclusões corretas por meio da análise de argumentos.
A proposição lógica nada mais é que o conteúdo de uma asserção, um enunciado, uma oração, que afirma algo.
Para que essa proposição possua valor lógico, esse “algo” precisa ser declarado como verdadeiro ou falso. Mas nunca as duas coisas.
Na hora da prova, uma dica importante: uma proposição lógica precisa ter um sujeito (algo que se declara) e um predicado (aquilo que se declara sobre o sujeito).
Quer um exemplo?
❌ O que não seria uma proposição?
As proposições na lógica obedecem a dois princípios fundamentais:
No entanto, também é preciso conhecer as categorias de proposições que podem surgir no Enem: as simples e compostas.
As proposições simples são mais fáceis de serem identificadas. Possuem somente uma oração que, como dissemos anteriormente, pode ser verdadeira ou falsa, mas não as duas.
Muitos estudiosos consideram a proposição simples o principal objeto de estudo da lógica.
Preposições simples se apresentam como nos exemplos abaixo:
Proposições compostas são aquelas formadas por mais de uma oração/sentença.
Por esse motivo, as proposições compostas precisam utilizar operadores lógicos (ou conectivos) para reunir suas diversas proposições simples.
Os operadores lógicos são aqueles conectivos que ajudam a formar uma proposição lógica composta, como:
Esses conectivos lógicos fazem parte de 5 estruturas lógicas:
Cada uma é representada por símbolo ou palavras que auxiliam na ligação de duas ou mais sentenças (gramaticalmente válidas), capazes de gerar uma nova sentença, composta somente dessas sentenças originais.
A seguir, vamos explicar cada uma dessas estruturas lógicas e mostraremos como você poderá identificar cada uma dentro de um exercício de raciocínio lógico na sua prova do Enem ou vestibular.
🔵 Leia também: As fórmulas de matemática mais importantes para o Enem
Pode aparecer representado pelo símbolo ∧ e, normalmente, pela letra “e”, como nos exemplos abaixo:
Nesse caso, duas proposições se unem para formar uma terceira. Porém, ela será verdadeira somente se as duas anteriores forem verdadeiras.
Para tornar mais fácil de aplicar nas provas, a tabela verdade pode ajudar a resolver essa questão (e você pode aplicá-la em sua prova):
| Situação | p | q | Resultado |
| -- | 73 | 53 | 73 ^ 53 |
| 1ª | V 73 é impar |
V 53 é menor que 73 |
V 73 é ímpar e 53 é menor que 73 |
| 2ª | V 73 é impar |
F 53 é maior que 73 |
F 73 é ímpar e 53 é maior que 73 |
| 3ª | F 73 é par |
V 53 é menor que 73 |
F 73 é par e 53 é menor que 73 |
| 4ª | F 73 é par |
F 53 é maior que 73 |
F 73 é par e 53 é maior que 73 |
Ou seja:
| p | q | p ^ q |
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
Além da conjunção “e”, algumas outras podem aparecer em exercícios com essa estrutura lógica, podendo substituir o “e”, tais como:
Pode aparecer representado pelo símbolo ∨ e pode ser traduzido pela palavra “ou”. Também é entendido como “inclusivo”.
No caso da disjunção, por conta do seu conectivo “ou”, ela sempre será verdadeira quando ao menos uma das proposições simples que compõe o enunciado seja verdadeira. Veja o exemplo:
Verifique as possíveis situações em que a disjunção é verdadeira ou falsa: “Eu vou estudar ou eu vou passear”. Primeiramente, identifique as proposições.
Novamente, crie a tabela, separando as proposições. Então, verifique as variáveis, tendo como base as informações que você possui.
| Situação | p | q | Eu vou estudar ou eu vou passear |
| -- | Eu vou estudar | Eu vou passear | p v q |
| 1ª | V | V | V |
| 2ª | F | V | V |
| 3ª | V | F | V |
| 4ª | F | F | F |
Ou seja:
| p | q | p v q |
| V | V | V |
| F | V | V |
| V | F | V |
| F | F | F |
❗Lembre-se: uma disjunção sempre será verdadeira quando ao menos uma das proposições simples que compõe o enunciado seja verdadeira. Caso ambas sejam falsas, a disjunção será falsa.
A negação é bastante simples de ser entendida. A negação inverte o valor lógico da proposição, tornando uma proposição verdadeira em uma proposição falsa (ou vice-versa), utilizando o conectivo “não”.
A negação também pode ser representada pelo símbolo ¬ ou ~ .
Primeiro é preciso entender se a proposição simples é verdadeira ou falsa. Para isso, é necessário reescrever a proposição.
Pode ser que a proposição já apresente o conectivo “não” (representado por ¬ p ou ~p). Nesse caso, a proposição negativa deve ser negada, ou seja, retirar o conectivo “não” da proposição (que passa a ser representado por p).
Caso o conectivo “não” já não esteja presente na proposição (p), deve ser realizado o movimento contrário, adicionando o conectivo “não” à proposição (~p).
Veja o exemplo:
| Situação | p | ~p |
| -- | 73 não é par | 73 é par |
| 1ª | V | F |
| 2ª | F | V |
❗ Lembre-se: (p) e (~p) nunca serão simultaneamente verdadeiros ou falsos. Isso acontece pois um é a contradição do outro.
A estrutura bicondicional é representada pelo símbolo ↔ ou pelo conectivo “se e somente se”.
Também reconhecida como equivalência, para que um enunciado seja uma estrutura lógica bicondicional verdadeira, a primeira e a segunda proposição, separadas pelo conectivo “se e somente se”, precisam ser ambas verdadeiras ou ambas falsas.
Na sentença “as estações do ano existem se somente se a Terra realizar o movimento de translação”, é preciso definir quantas possibilidades verdadeiras e falsas existem.
Primeiro, como sempre, é preciso nomear as proposições que fazem parte da sentença.
Vamos agora expor as possibilidades de a bicondicional ser considerada verdadeira ou falsa com a ajuda da tabela da verdade.
| Situação | p | q | As estações do ano existem se somente se a Terra realizar o movimento de translação |
| -- | As estações do ano existem | a Terra realizar o movimento de translação. | p ↔ q |
| 1ª | V | V | V |
| 2ª | F | V | F |
| 3ª | V | F | F |
| 4ª | F | F | V |
Ou seja:
Na estrutura condicional, o nome já ajuda a entender sua lógica. É representada pelo símbolo → ou “se… então…”. O conectivo “se” identifica a proposição chamada antecedente e o conectivo “então” identifica a preposição consequente.
Uma proposição composta condicional sempre será falsa se a primeira proposição da sentença for verdadeira e a segunda for falsa (p → q, ou “se p é verdadeiro, então q é falso”), o que pode ser entendido como uma quebra da condicional.
Em qualquer outro caso, a proposição composta condicional será verdadeira.
Suponha uma questão em que é preciso mostrar em quais situações a seguinte frase “se nasci no Brasil, então sou brasileiro” possui a condicional como sendo verdadeira ou falsa.
Novamente, é preciso identificar as proposições.
A tabela da verdade, mais uma vez, nos fornece a resposta que buscamos:
| Situação | p | q | Se nasci no Brasil, então sou brasileiro |
| -- | nasci no Brasil | sou brasileiro | p → q |
| 1ª | V | V | V |
| 2ª | F | V | V |
| 3ª | V | F | F |
| 4ª | F | F | V |
Ou seja:
🔵 Leia também: Quantos pontos precisa para passar no ENEM?
Você acabou de entender um pouco mais sobre o raciocínio lógico, desde sua origem na Filosofia, na Antiguidade, até sua aplicação na Matemática e, consequentemente, como parte importante da prova do Enem e outros vestibulares e concursos.
Demos alguns exemplos e dicas importantes, que vão te ajudar a identificar os melhores caminhos para entender as questões e resolvê-las da melhor maneira.
Para você praticar, separamos 3 questões de raciocínio lógico que caíram nos últimos anos no Enem. Elas foram retiradas do banco de provas e gabaritos do Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep), órgão do Ministério da Educação (MEC) responsável pela realização do Exame.
Não se esqueça de ler com atenção os enunciados e de utilizar a tabela verdade. Ela pode ajudar a resolver grande parte das questões.
Bons estudos!
No projeto de uma nova máquina, um engenheiro encomendou a um torneiro mecânico a fabricação de uma peça, obtida a partir do recorte em um cubo, como ilustrado na figura. Para isso, o torneiro forneceu, juntamente com o desenho tridimensional da peça, suas vistas frontal, lateral e superior, a partir das posições indicadas na figura. Para facilitar o trabalho do torneiro, as arestas dos cortes que ficam ocultos nas três vistas devem ser representadas por segmentos tracejados, quando for o caso.
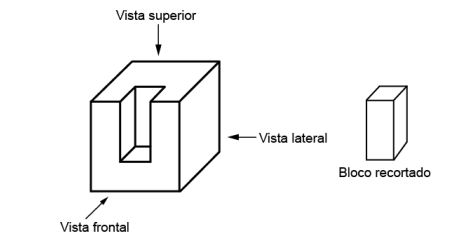
As vistas frontal, lateral e superior que melhor representam o desenho entregue ao torneiro são
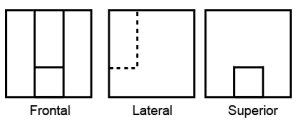
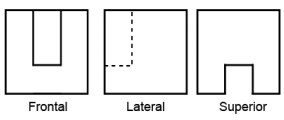
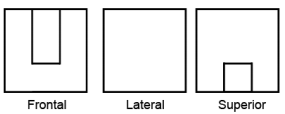
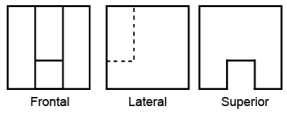
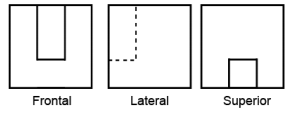
✅ Gabarito: E
Um casal planejou uma viagem e definiu como teto para o gasto diário um valor de até R$ 1 000,00. Antes de decidir o destino da viagem, fizeram uma pesquisa sobre a taxa de câmbio vigente para as moedas de cinco países que desejavam visitar e também sobre as estimativas de gasto diário em cada um, com o objetivo de escolher o destino que apresentasse o menor custo diário em real.
O quadro mostra os resultados obtidos com a pesquisa realizada.
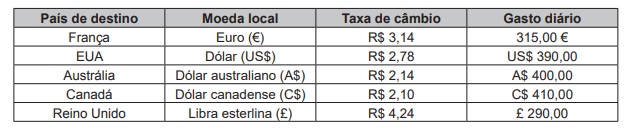
Nessas condições, qual será o destino escolhido para a viagem?
✅ Gabarito: A
Na teoria das eleições, o Método de Borda sugere que, em vez de escolher um candidato, cada juiz deve criar um ranking de sua preferência para os concorrentes (isto é, criar uma lista com a ordem de classificação dos concorrentes). A este ranking é associada uma pontuação: um ponto para o último colocado no ranking, dois pontos para o penúltimo, três para o antepenúltimo, e assim sucessivamente. Ao final, soma-se a pontuação atribuída a cada concorrente por cada um dos juízes.
Em uma escola houve um concurso de poesia no qual cinco alunos concorreram a um prêmio, sendo julgados por 25 juizes. Para a escolha da poesia vencedora foi utilizado o Método de Borda. Nos quadros, estão apresentados os rankings dos juízes e a frequência de cada ranking.

A poesia vencedora foi a de
✅ Gabarito: E
2023 © BLOG DO EAD | Todos os Direitos Reservados