Questões abordando geometria plana e espacial aparecem em todas as edições do Enem, então perguntamos: você sabe como responder essas questões?
A geometria é a área da matemática que estuda formas geométricas em comprimento, área e volume. Dentro dessa área existem três categorias: e a geometria analítica, plana e espacial.
Sendo que a geometria plana e espacial são duas categorias que analisam figuras no plano e no espaço. A primeira focando em objetos em duas dimensões e a segunda, objetos em três dimensões.
Neste artigo, nós vamos explorar o tema da geometria plana e espacial para ajudar você a praticar para o Enem.
Por isso, vamos falar sobre o que mais cai na prova de matemática, o que são a geometria plana e espacial e questões para você estudar.
Você vai conferir:
O que mais cai em matemática no Enem
A prova do Enem reúne conteúdos presentes no currículo escolar do ensino médio.
Esses conteúdos foram divididos na prova em quatro áreas do conhecimento:
- Ciências Humanas e suas Tecnologias;
- Ciências da Natureza e suas Tecnologias;
- Linguagens, Códigos e suas Tecnologias;
- Matemática e suas Tecnologias.
Cada área conta com 45 questões objetivas no Enem, ou seja, o exame tem 180 perguntas no total.
Existe um documento elaborado pelo Ministério da Educação (o MEC), a Matriz de Referência do Enem , onde você pode conferir todas as matérias que caem na prova de Matemática e suas Tecnologias.
Diferente das outras provas, essa área do conhecimento não aborda mais do que uma disciplina. A prova de matemática e suas tecnologias foca na matemática.
Abaixo, fizemos um breve levantamento dos conteúdos que mais caem :
- Equações e funções de 1° e 2° grau
- Porcentagem
- Geometria plana e espacial
- Regra de três
- Matemática financeira
- Razões e proporções
- Noções de estatística
- Circunferências
- Leitura e interpretação de gráficos
Dentre esses, geometria plana e espacial é um assunto recorrente na prova.
Qual é a diferença entre geometria plana e espacial?
Embora a geometria plana e espacial partam do mesmo ponto, o estudo de figuras, elas se diferem porque estudam diferentes dimensões.
A geometria plana é o estudo de figuras em duas dimensões, como quadrados, círculos, retângulos e triângulos.
Enquanto a geometria espacial estuda figuras em três dimensões, ou seja, cubos, esferas, paralelepípedos e pirâmides.
O que são conceitos primitivos da geometria?
Os conceitos primitivos são a base da geometria, em cima do que ela é construída, porém são conceitos sem definição.
E embora não tenham uma definição, nós conseguimos entender o que são esses conceitos primitivos e como eles se relacionam.
Estes são os conceitos primitivos:
- Ponto : é a base de toda a geometria porque é a partir de um conjunto de pontos que se constrói figuras. Ele é usado para representar localizações no espaço e, usualmente, nós o desenhamos como uma “bolinha”, um pingo de tinta no papel.
- Reta : são conjuntos de pontos entendidos como linhas sem curvas. É possível dizer que a reta é a distância entre dois pontos, porém não é possível determinar a largura de uma reta porque pontos não têm largura. Então, as retas são determinadas como objetos unidimensionais, que têm apenas uma dimensão.
- Plano : é um conjunto infinito e ilimitado de retas. Costumam ser superfícies retas e é dentro deles que são definidas figuras bidimensionais, ou seja, que tem duas dimensões. Isso significa que as figuras presentes dentro de um plano podem ter comprimento e largura. É aqui que a geometria plana acontece.
- Espaço : e assim como o plano é a justaposição de retas, o espaço é a justaposição de planos. Ou seja, são planos colocados um sobre o outro, tão próximos que podem ser confundidos. Nesse espaço, podem ser construídas figuras tridimensionais, ou seja, em três dimensões. Isso porque o espaço permite uma terceira dimensão, a altura. É aqui que acontece a geometria espacial.
É importante dizer que, embora não se tenha uma definição conceitual para os conceitos primitivos, nós ainda podemos tentar defini-los a partir de sua formação e características.
O que é a geometria plana?
A geometria plana, também conhecida como euclidiana, é o estudo de figuras em duas dimensões, aquelas que não possuem volume.
Ela foi criada pelo matemático Euclides de Alexandria e explora a propriedade e os tamanhos de figuras planas aplicando fórmulas matemáticas para encontrar sua área e perímetro.
Principais conceitos da geometria plana
Além dos conceitos primitivos já citados, existem outros conceitos que ajudam a formar a geometria plana. São eles:
- Semirretas : retas que não possuem fim, ou seja, que têm apenas sentido e direção, mas sem indicação de origem.
- Segmento de retas : retas divididas em dois pontos que têm tamanhos definidos. Estas podem ser classificadas em quatro: consecutivas, colineares, adjacentes e congruentes.
- Ângulos : a junção entre dois segmentos de retas, que possuem grau de abertura. Podem ser classificados em cinco: nulo, agudo, reto, obtuso e raso.
- Área : é todo o tamanho da superfície da figura.
- Perímetro : é o resultado da soma dos comprimentos, ou seja, a soma de todos os lados da figura.
Classificação das figuras geométricas planas
Figuras planas são superfícies que possuem comprimento e largura, não possuindo volume.
São formadas por segmentos de retas e classificadas entre polígonos e não polígonos.
- Polígonos: são figuras fechadas e formadas por segmentos de retas;
- Não polígonos : abertos ou fechados, são formados totalmente por segmentos de retas.
Dentro das figuras planas também existem os paralelogramos , que são formas de quatro lados iguais cujos lados opostos são paralelos. Por exemplo, um retângulo.
As figuras geométricas planas são:
Triângulo
O triângulo é uma figura plana formada por três segmentos de retas, tendo três lados, e ângulos internos que somam 180°. Existem três classificações de triângulos:
- Equilátero : quando todos os lados são iguais e os ângulos internos têm 60°;
- Isósceles : apenas dois dos lados e ângulos do triângulo são iguais, o terceiro diverge;
- Escaleno : onde todos os lados do triângulo são diferentes.
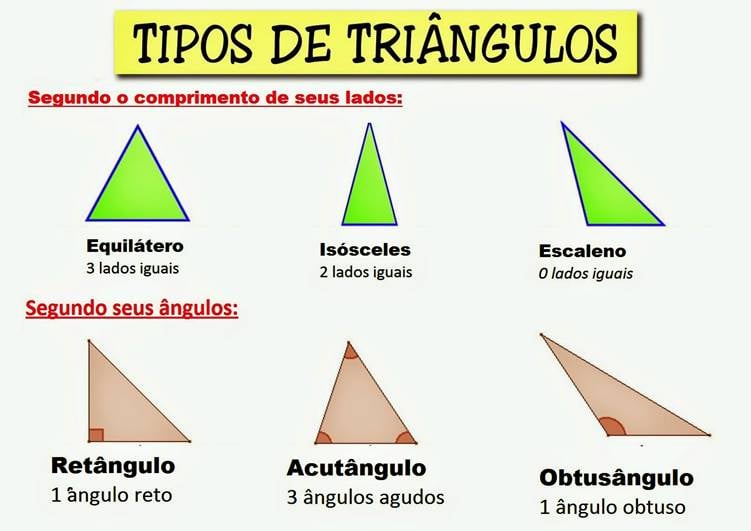
Fonte: trabalhosparaaescola.com.br
Existe também uma classificação dos triângulos de acordo com seus ângulos.
- Triângulo retângulo : tem ângulo interno igual a 90°;
- Triângulo obtusângulo : possui dois ângulos agudos, menores que 90°;
- Triângulo acutângulo : possui três ângulos menores que 90°.
Quadrado
O quadrado é um polígono que tem quatro lados iguais, quatro segmentos de retas, e está presente no grupo dos quadriláteros, figuras com quatro lados. Possui ângulos internos retos (90°) e iguais.
Retângulo
O retângulo é um paralelogramo que tem todos os ângulos internos retos, ou seja, com 90°. Ele possui quatro lados, porém seus lados divergem de tamanho.
Os lados verticais e horizontais são paralelos entre si.
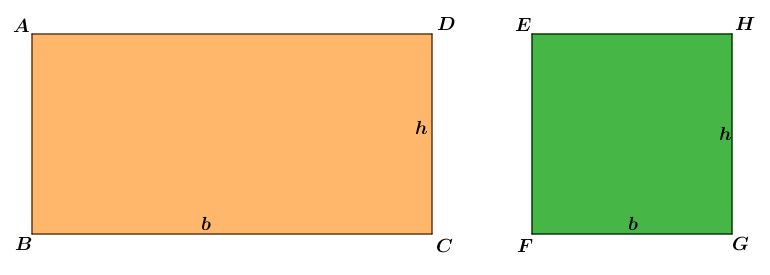
Fonte: infoescola.com
Trapézio
O trapézio também é um paralelogramo que possui seis lados. A soma de seus ângulos internos chega a 360°.
Como principal característica, o trapézio tem bases paralelas, uma maior do que a outra, e lados paralelos. Pode ser classificado como:
- Trapézio Retângulo : quando possui ângulos internos de 90°;
- Trapézio isósceles : quando um dos lados não paralelos tem dimensão divergente;
- Trapézio Escaleno : quando todos os lados são diferentes.
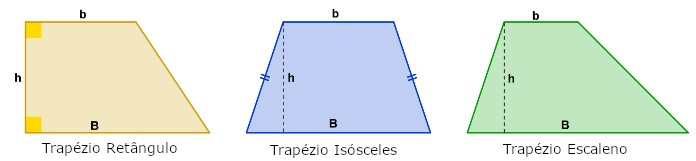
Fonte: infoescola.com
Losango
O losango também é um paralelogramo e um quadrilátero, porém ele possui diagonais paralelas que formam um ângulo de 90°.
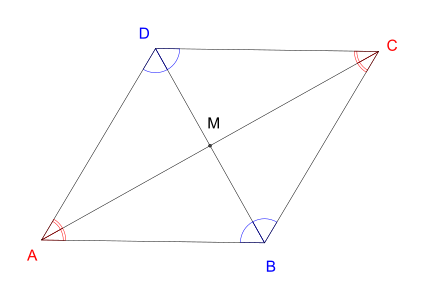Fonte: wikipedia.org
Círculo
Já o círculo não é um paralelogramo, nem um quadrilátero e nem um polígono. O círculo é um não polígono, pois é uma figura formada apenas de pontos no plano.
Ele é composto pelo raio (r), que é o valor da distância entre o centro do círculo e seu contorno.
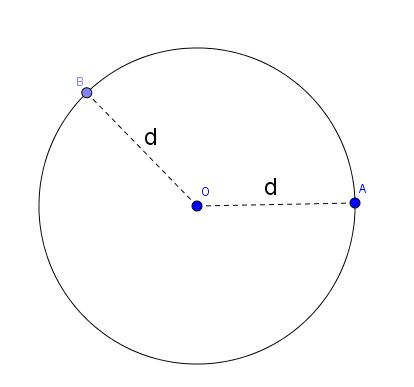Fonte: infoescola.com
Fórmulas da geometria plana
Cada uma das figuras descritas acima têm uma fórmula específica para que seja calculada sua área.
Vamos ver cada uma delas:
Triângulo
Existem algumas fórmulas diferentes, dependendo da classificação do triângulo.
Por exemplo, para calcular a área do triângulo retângulo, é preciso multiplicar a base e altura e dividir por dois. A fórmula é a seguinte: A = b*h / 2 (Sendo A , área, b , base e h , altura).
Já no cálculo para triângulos equiláteros, a fórmula é a seguinte: A = l² * √3 / 2 (Sendo A , a área e l , o lado).
Já para calcular a área de triângulos com ângulos internos menores do que 90°, podemos usar trigonometria (cosseno, seno e semiperímetro).
Retângulo
Para encontrar a área do retângulo, você precisa multiplicar a base pela altura. A fórmula fica assim: A = b*h (Sendo A , a área, b , a base e h , a altura).
Quadrado
Para encontrar a área do quadrado, você precisa encontrar a medida de um dos lados e elevar ao quadrado. Ou seja: A = l² (Sendo A representando a área e l , lado).
Trapézio
A área do trapézio é encontrada multiplicando a altura pela soma da base maior com a menor e dividindo por dois.
Na fórmula: A = (B+b)*2 / 2 (Sendo A , a área, B , a base maior e b , a base menor).
Losango
Para encontrar a área do losango, é preciso multiplicar a diagonal maior pela menor e dividir por dois.
Como na fórmula: A = D*d / 2 (Sendo A , a área, D, a diagonal maior e d , a diagonal menor).
Círculo
O cálculo da área do círculo possui uma constante, o Pi (π), aproximadamente 3,14.
Por isso, para encontrar a área do círculo bastante elevar o raio ao quadrado e multiplicar por π. Ou seja: A = π*r² (Sendo A , área e r , raio).
O que é a geometria espacial?
Já a geometria espacial é o estudo de figuras sólidas no espaço, ou seja, figuras em três dimensões.
Elas possuem comprimento, largura e altura ou comprimento, largura e profundidade.
A ideia de geometria espacial é muito antiga, sendo que o povo Egípcio já a utilizava, como podemos ver no Papiro de Rhind e no Papiro de Moscou.
Os documento datam de cerca de 1650 a.C., e podemos ver a resolução de cálculos do volume de poliedros.
Principais conceitos da geometria espacial
Assim como a geometria plana, a geometria espacial também utiliza os conceitos primitivos, já que eles são a base de toda a geometria.
Porém, a geometria espacial também tem seus próprios conceitos:
- Aresta : são os segmentos de retas que ligam os dois vértices de uma figura;
- Vértice : é o local onde se encontram duas ou mais arestas;
- Face : são os polígonos que formam a figura, ou seja, um dos lados.
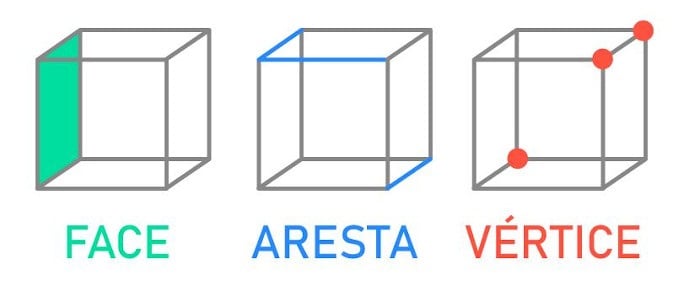
Fonte: escolakids.uol.com.br
Além disso, a geometria espacial também tem conceitos que abrangem as posições relativas entre os conceitos primitivos.
Ou seja, como pontos, retas e planos se relacionam dentro do espaço.
- Posição relativa entre ponto e reta, e ponto e plano : o ponto pode pertencer à reta e/ou ao plano, ou não;
- Posição relativa entre pontos : dois ou mais pontos podem pertencer à uma mesma reta e/ou a um mesmo plano, ou não;
- Posição relativa entre duas retas : retas que estão no mesmo plano podem ser paralelas (quando não têm nenhum ponto em comum), concorrentes (quando têm um ponto em comum) e coincidentes (quando são iguais, existindo apenas uma reta). E quando duas retas não pertencem ao mesmo plano, elas são chamadas de retas reversas.
- Posições relativas entre dois planos : existem os planos paralelos (quando não possuem nenhum elemento em comum), plano secantes (quando eles se interceptam) e os planos coincidentes (quando são iguais, ou seja, apenas um plano).
- Posição relativa entre uma reta e um plano : a reta pode ser secante ao plano (quando ela corta o plano e tem apenas um ponto em comum com ele), pertencente ao plano (quando todos os pontos da reta estão dentro do plano) e paralela ao plano (quando nenhum ponto da reta pertence ao plano).
Os Sólidos de Platão (e Fórmula de Euler)
Dentro das figuras espaciais ainda existem os Sólidos de Platão.
Este conceito nasceu do desejo do filósofo de explicar o universo a partir da geometria.
Então, ele associou cinco sólidos geométricos à natureza. São eles:
- Tetraedro : é o poliedro regular com menos lados, associado por Platão ao elemento fogo;
- Cubo (ou Hexaedro) : possui seis faces quadradas e era associado ao elemento terra por Platão;
- Octaedro : figura de oito faces, associada ao ar por Platão;
- Icosaedro : com 20 faces, essa figura possui faces triangulares e era associada ao elemento água por Platão;
- Dodecaedro : figura de dez faces, considerado por Platão como o mais harmonioso dos poliedros. Logo, ele o associava com o universo.
Fonte: escolaeducacao.com.br
Analisando os sólidos de Platão, Euler, um matemático, chegou a uma fórmula que pode ser usada para encontrar qualquer um dos três elementos de um poliedro convexo (arestas, vértice e face).
Esta é a fórmula de Euler:
- V – A + F = 2 (Sendo V , vértice, A , aresta e F , face).
Corpos redondos (ou Sólidos de Revolução)
Também existe dentro da geometria espacial, uma classificação de figuras tridimensionais que possuem a base redonda, ou seja, um círculo.
Elas são construídas a partir da rotação de um círculo e podem ser: esferas, cilindros e cones.
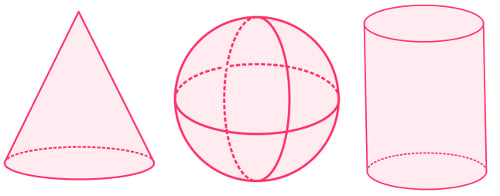Fonte: mundoeducacao.uol.com.br
Classificação das figuras geométricas espaciais
As figuras espaciais são formadas por pontos e retas, possuem comprimento, largura e altura (às vezes, comprimento, largura e profundidade) e têm volume.
Elas podem ser classificadas como poliedros e não poliedros:
- Poliedros : sólidos fechados formados por superfícies, ou faces, planas;>
- Não poliedros : sólidos nem sempre formados por superfícies planas, podem ser curvas.
Dentro da classificação dos poliedros, ainda existe a classificação entre convexo e côncavo .
Os poliedros côncavos são aqueles cujas faces não estão contidas no semiespaço. Já os poliedros convexos são aqueles que têm faces que se encontram totalmente no semiespaço.
Ainda dentro dos poliedros convexos, eles podem ser regulares (como os sólidos de Platão, que tem faces iguais) ou irregulares.
Os poliedros irregulares são formados por faces divergentes, como as pirâmides e os prismas, que têm faces de tamanhos e formas diferentes.
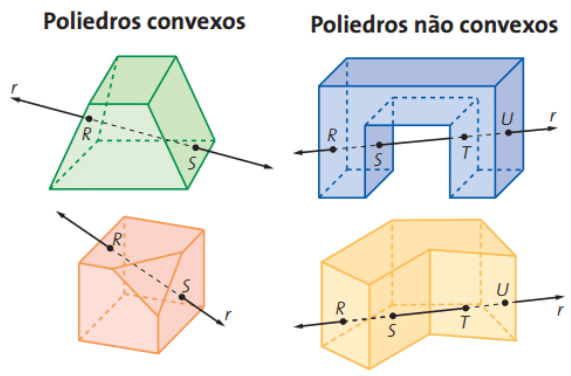Fonte: casadamatematica.com.br
De acordo com o número de faces, os poliedros são classificados dessa maneira:
- Tetraedro : quatro faces;
- Pentaedro : cinco faces;
- Hexaedro : seis faces;
- Heptaedro : sete faces;
- Octaedro : oito faces;
- Decaedro : dez faces;
- Dodecaedro : doze faces;
- Icosaedro : vinte faces.
E assim por diante. Por exemplo, uma figura de 30 faces é chamada de Triacontágono .
Fórmulas da geometria espacial
Cada figura dentro da geometria especial tem uma fórmula própria e os cálculos mais comuns envolvem descobrir a área total (At) e o volume (V - não confundir com o vértice, que na Fórmula de Euler também é V).
Vamos ver todas elas:
Pirâmides
As pirâmides são sólidos formados por uma base poligonal, ou seja, uma figura plana fechada formada por pontos e retas, e um vértice que une todas as arestas.
As pirâmides podem ser classificas de acordo com sua inclinação: retas, quando tem ângulo de 90°, e oblíquas, quando tem ângulos diferentes de 90°.
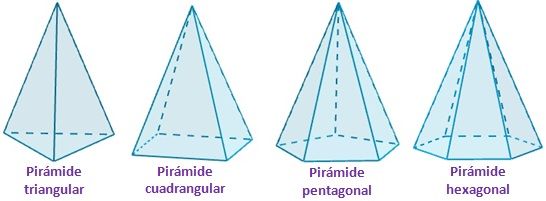Fonte: conhecimentocientifico.com
As fórmulas das pirâmides são:
- Área total: Al + Ab
- Volume: 1/3 Ab.h
Sendo At , a área total, Al , a área lateral, Ab , a área da base e h , a altura.
Prismas
Os prismas são formados por duas faces planas que tem o mesmo tamanho e forma e laterais compostas por paralelogramos, cujos lados opostos são iguais, ou quadriláteros.
Podem ser classificados de acordo com inclinação como retos ou oblíquos. Cubos e paralelepípedos estão dentro dessa categoria.
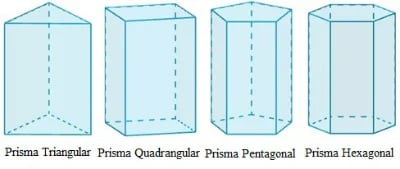Fonte: todamateria.com.br
As fórmulas para calcular a área total e volume dos prismas são:
- Área da Face: a.h
- Área Lateral: 6.a.h
- Área da base: 3.a3v3/2
- Volume: Ab.h
Sendo que a área da base é representada por Ab , a área, por a , e a altura por h.
Corpos redondos
Os corpos redondos, como explicamos acima, são figuras com bases circulares. São eles os cones, cilindros e esferas.
Também podem ser classificados como retos e oblíquos, dependendo de seus ângulos.
As fórmulas são as seguintes:
- Área lateral: Al = 2.p.r.h
- Área da base: Ab = p.r²
- Área total: At = Al + 2.Ab ou At = 2.p.r(h + r)
- Volume: V = Ab.h
Sendo que At é a área total, Ab é a área da base, Al é a área lateral, p é o Pi, r é o raio, h é a altura e V , volume.
Exercícios do Enem sobre geometria plana e espacial para você praticar
Certo, agora que você já entendeu o que é a geometria plana e espacial e já conferiu conceitos e fórmulas, vamos aos exercícios.
Este é um conteúdo que sempre aparece no Enem, então reunimos algumas questões que já passaram pela prova para você praticar.
Confira as respostas na conclusão deste artigo. Vamos lá:
Questão 1
Em canteiros de obras de construção civil, é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo conforme pode ser visto na figura, em que as estacas foram indicadas por letras.
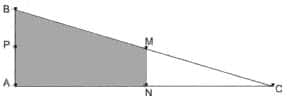
A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto. Nessas condições, a área a ser calçada corresponde
- à mesma área do triângulo AMC.
- à mesma área do triângulo BNC.
- à metade da área formada pelo triângulo ABC.
- ao dobro da área do triângulo MNC.
- ao triplo da área do triângulo MNC.
Questão 2
Num recipiente com a forma de paralelepípedo reto-retângulo, colocou-se água até a altura de 8 cm e um objeto, que ficou flutuando na superfície da água. Para retirar o objeto de dentro do recipiente, a altura da coluna de água deve ser de, pelo menos, 15 cm. Para a coluna de água chegar até essa altura, é necessário colocar dentro do recipiente bolinhas de volume igual a 6 cm3 cada, que ficarão totalmente submersas.
O número mínimo de bolinhas necessárias para que se possa retirar o objeto que flutua na água, seguindo as instruções dadas, é de
- 14.
- 16.
- 18.
- 30.
- 34.
Conclusão
Chegando ao final deste artigo, esperando que você tenha conseguido tirar suas dúvidas sobre os conteúdos de geometria plana e espacial que caem no Enem.
Confira as respostas das questões acima:
- Questão 1 - e) ao triplo da área do triângulo MNC.
- Questão 2 - a) 14 bolinhas.
×
Relacionados
Categorias