Todos os anos, o Exame Nacional do Ensino Médio (Enem) acontece em dois finais de semana consecutivos, geralmente no mês de novembro.
O formato tradicional conta com 180 questões de múltipla escolha e mais uma redação.
A estatística é um dos conteúdos que mais aparecem nas provas, principalmente na área de matemática , junto com as funções e as grandezas diretamente e inversamente proporcionais.
Contudo, esse assunto pode fazer parte de outras disciplinas, como em Ciências da Natureza, e até mesmo na redação, a partir da interpretação de dados estatísticos em gráficos ou tabelas.
Para te ajudar, trouxemos 5 exercícios resolvidos de estatística do Enem.
Vamos praticar?
O que é estatística
O primeiro passo é ter em mente o que é a estatística e como ela é aplicada.
Em suma, é uma das áreas da matemática que mais se encaixa na área social, pois estuda dados, os coleta, os organiza e os analisa, além de representá-los de maneira gráfica ou explicá-los de outra forma.
Para esclarecer ainda mais a importância da estatística, podemos pensar que, com ela, foi possível ter uma base de dados a respeito da pandemia de Covid-19, orientando toda a sociedade sobre curvas de contágio, por exemplo, além de ter movimentado decisões políticas e sociais a respeito da doença e como superá-la.
Junto do assunto de probabilidade, a estatística faz parte da competências 6 do Enem.
Com a probabilidade, a estatística compõe a competência 6 do Enem , que é definida por:
Competência de área 6 - Compreender e usar os sistemas simbólicos das diferentes linguagens como meios de organização cognitiva da realidade pela constituição de significados, expressão, comunicação e informação.
As questões variam entre médias e fáceis, mas não é impossível cair uma de nível difícil dessa área, por isso, vale a pena afiar o conhecimento para evitar apuros na prova de matemática do Enem.
Como interpretar estatísticas
Para saber interpretar as estatísticas, é preciso ter em mente quais são os principais conceitos englobados no tema. São eles:
- População: numa cidade, estado ou país, é o número de pessoas que ali estão. Ou também o conjunto de elementos.
- Amostra: parte representativa de uma população.
- Variável: elemento representante do conjunto de todos os resultados possíveis de um fenômeno.
- Frequência absoluta: vezes que o valor da variável é citado.
- Frequência relativa: é apresentado em porcentagem. É encontrado pela divisão entre a frequência absoluta de cada variável e o somatório das frequências absolutas.
Medidas de Tendência Central
- Média aritmética: somatório dos valores dos itens, dividido pelo número de itens.
- Média aritmética ponderada: somatório dos valores dos elementos multiplicado pelos seus respectivos pesos, dividido pela soma dos pesos atribuídos.
- Moda: valor que mais aparece ou se repete numa série.
- Mediana: medida central em uma determinada sequência de números.
Medidas de Dispersão
- Amplitude: subtração entre o maior e o menor valor dos itens do conjunto.
- Variância: dispersão dos dados variáveis em relação à média.
- Desvio Padrão: raiz quadrada da variância.
Após entender esses conceitos, é essencial, para que você possa interpretar, que fique claro como esses dados podem ser apresentados e como encarar isso.
Mas já adiantamos: a leitura é uma aliada nessa hora.
Leia tudo com atenção, seja os valores, texto-base, enunciado, legendas e demais elementos que você pode se munir para obter e entender as informações necessárias.
Se os números ou informações forem apresentados num gráfico, por exemplo, verifique qual é o formato desse gráfico: é de barras? Estilo “pizza”? Ou seria de colunas?
Cada um desses modelos exibe os dados de maneira diferente, então é preciso ficar atento com cores, tamanhos e números.
Os eixos e suas indicações precisam de muita atenção. As legendas estão lá para te orientar: foque nelas para não deixar nada passar batido.
Ter em mente quais são os maiores e menores valores apresentados no gráfico também ajuda.
Se as informações aparecerem numa tabela, as orientações anteriores também funcionam.
Também vale entender a disposição das informações, o que cada coluna apresenta e o que cada linha significa.
O título das tabelas e dos gráficos também deve ser compreendido pelo participante.
Outro ponto importantíssimo: as informações podem ser colocadas em textos também.
Para interpretar, uma dica que damos é ler com atenção e sublinhar os valores colocados.
Se possível, anote os dados numa folha de rascunho para ter tudo em mãos na hora de fazer o que o enunciado pede.
Falando nisso, a orientação da atividade precisa ser lida com calma e você precisa ficar de olho para não trocar as informações.
Entender o contexto das informações, através do texto-base, faz com que a interpretação dos dados aconteça de maneira mais fácil também.
Exercícios de estatística para se preparar para o Enem
Agora que você já leu os principais conceitos de estatística e como interpretar corretamente os dados dispostos, vamos praticar!
Disponibilizamos alguns exercícios e respostas para você treinar seu conhecimento em estatística. Vamos lá?
1) Enem – 2017
A avaliação de rendimento de alunos de um curso universitário baseia-se na média ponderada das notas obtidas nas disciplinas pelos respectivos números de créditos, como mostra o quadro:
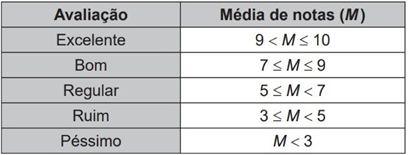
Quanto melhor a avaliação de um aluno em determinado período letivo, maior sua prioridade na escolha de disciplinas para o período seguinte.
Determinado aluno sabe que se obtiver avaliação “Bom” ou “Excelente” conseguirá matrícula nas disciplinas que deseja.
Ele já realizou as provas de 4 das 5 disciplinas em que está matriculado, mas ainda não realizou a prova da disciplina I, conforme o quadro.
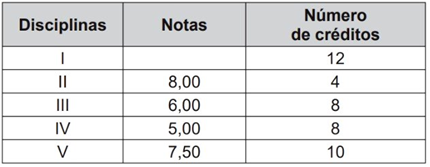
Para que atinja seu objetivo, a nota mínima que ele deve conseguir na disciplina I é
- 7,00.
- 7,38.
- 7,50.
- 8,25.
- 9,00.
✅ Resposta - Alternativa d) 8,25:
Para calcular a média ponderada, vamos multiplicar cada nota pelo seu respectivo número de créditos, depois somar todos os valores encontrados e por fim, dividir pelo número total de créditos.
Através da primeira tabela, identificamos que o aluno deverá atingir pelo menos a média igual a 7 para obter a avaliação "bom". Portanto, a média ponderada deverá ser igual a esse valor.
Chamando a nota que falta de x, vamos resolver a seguinte equação:
2) Enem – 2017
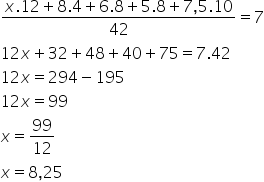
Três alunos, X, Y e Z, estão matriculados em um curso de inglês. Para avaliar esses alunos, o professor optou por fazer cinco provas.
Para que seja aprovado nesse curso, o aluno deverá ter a média aritmética das notas das cinco provas maior ou igual a 6. Na tabela, estão dispostas as notas que cada aluno tirou em cada prova.
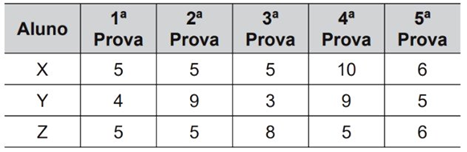
Com base nos dados da tabela e nas informações dadas, ficará(ão) reprovado(s)
- apenas o aluno Y.
- apenas o aluno Z.
- apenas os alunos X e Y.
- apenas os alunos X e Z.
- os alunos X, Y e Z.
✅ Resposta - Alternativa: b) apenas o aluno Z:
A média aritmética é calculada somando-se todos os valores e dividindo-se pelo número de valores. Neste caso, vamos somar as notas de cada aluno e dividir por cinco.
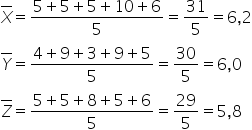
Como o aluno ficará aprovado com nota igual ou superior a 6, então os alunos X e Y serão aprovados e o aluno Z reprovado.
3) Enem – 2017
O gráfico apresenta a taxa de desemprego (em %) para o período de março de 2008 a abril de 2009, obtida com base nos dados observados nas regiões metropolitanas de Recife, Salvador, Belo Horizonte, Rio de Janeiro, São Paulo e Porto Alegre.
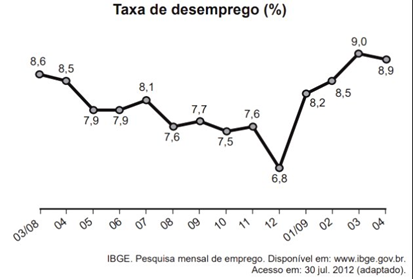
A mediana dessa taxa de desemprego, no período de março de 2008 a abril de 2009, foi de
- 8,1%
- 8,0%
- 7,9%
- 7,7%
- 7,6%
✅ Resposta - Alternativa: b) 8,0%:
Para encontrar o valor da mediana, devemos começar colocando todos os valores em ordem. Em seguida, identificamos a posição que divide o intervalo em dois com o mesmo número de valores.
Quando o número de valores for ímpar, a mediana será o número que está exatamente no meio do intervalo. Quando for par, a mediana será igual a média aritmética dos dois valores centrais.
Observando o gráfico, identificamos que existem 14 valores relativos à taxa de desemprego. Como 14 é um número par, a mediana será igual a média aritmética entre o 7º valor e o 8º valor.
Desta forma, podemos colocar os números em ordem até chegar a essas posições, conforme apresentado abaixo:
6,8; 7,5; 7,6; 7,6; 7,7; 7,9; 7,9; 8,1
Calculando a média entre o 7,9 e o 8,1, temos:
4) Enem – 2015
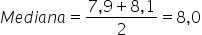
Em uma seletiva para a final dos 100 metros livres de natação, numa olimpíada, os atletas, em suas respectivas raias, obtiveram os seguintes tempos:
A mediana dos tempos apresentados no quadro é
- 20,70.
- 20,77.
- 20,80.
- 20,85.
- 20,90.
✅ Resposta - Alternativa: d) 20,85:
Primeiro, vamos colocar todos os valores, inclusive os números repetidos, em ordem crescente:
20,50; 20,60; 20,60; 20,80; 20,90; 20,90; 20,90; 20,96
Observe que existe um número par de valores (8 tempos), assim, a mediana será a média aritmética entre o valor que está na 4º posição e o da 5º posição:
5) Enem – 2014
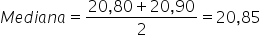
Os candidatos K, L, M, N e P estão disputando uma única vaga de emprego em uma empresa e fizeram provas de português, matemática, direito e informática. A tabela apresenta as notas obtidas pelos cinco candidatos.
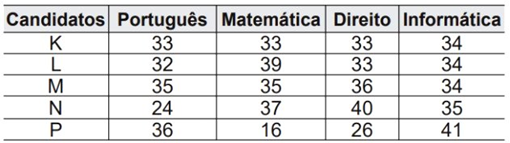
Segundo o edital de seleção, o candidato aprovado será aquele para o qual a mediana das notas obtidas por ele nas quatro disciplinas for a maior. O candidato aprovado será
- K.
- L.
- M.
- N.
- P.
✅ Resposta - Alternativa: d) N:
Precisamos encontrar a mediana de cada candidato para identificar qual é a maior. Para isso, vamos colocar as notas de cada um em ordem e encontrar a mediana.
Candidato K:
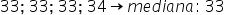
Candidato L:
Candidato M:
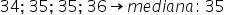
Candidato N:
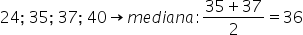
Candidato P:
Conclusão
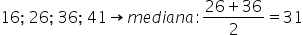
E aí, preparado para arrasar em estatística no Enem? Esperamos que sim!
Não deixe de continuar praticando e testando seus conhecimentos nesta e em outras áreas.
Faça um bom e estruturado plano de estudo para nenhum tema-chave ficar de fora, busque provas antigas para se embasar e fique sempre atento às atualidades e notícias, além de ler todo o edital.
Para ajudar, deixamos aqui um checklist do Enem , com tudo que você precisa saber! Também separamos mais alguns exercícios de matemática para você fixar o conteúdo.
Boa prova!
×
Relacionados
Categorias