

Lorem ipsum dolor sit amet, consectetur adipiscing elit
Acompanhe
Como estão os estudos para o Exame Nacional do Ensino Médio?
O Enem acontece todos os anos em dois finais de semana consecutivos, geralmente em novembro, com o formato tradicional de 180 questões de múltipla escolha e mais uma redação.
Matemática e suas tecnologias é a única prova que apresenta uma disciplina isolada, o que a deixa com o maior peso individual do Exame.
São 45 questões objetivas com enunciados que abordam temas descritos no Programa de Prova disponível no site do Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep) , órgão do Ministério da Educação (MEC) responsável pela realização do Enem.
Um desses temas abrange os polígonos, tanto os convexos quanto os não convexos, também chamados de côncavos.
A palavra “polígonos” vem da união dos termos gregos "poly" e "gon", resultando no significado "muitos ângulos".
Mas o que são, de fato, os polígonos?
Essas figuras geométricas planas, formadas por lados, são feitas por uma única linha fechada.
São exemplos de polígonos: triângulo, quadrado, hexágono, entre outros. O nome dos polígonos deriva de sua quantidade de lados.
Confira a nomenclatura abaixo:
Os polígonos podem ser convexos ou não convexos, baseando-se no formato dessa linha única que falamos há pouco.
Vamos falar mais sobre essas classificações a seguir.
Para verificar que possui extremidades no interior do polígono, estão dentro dele. Se sim, tem-se um polígono convexo.
Já se tiver ao menos um segmento de reta com as extremidades dentro do polígono e, também, um ponto fora dele, esse polígono não será convexo.
Sendo assim, a diferença entre os dois modelos de polígonos consiste na posição das extremidades do segmento de reta.
Também é possível verificar a diferença analisando a amplitude dos ângulos internos do polígono.
Funciona assim: se todos os ângulos internos forem menores que 180º então o polígono é convexo, contudo, se pelo menos um ângulo for maior que 180º, ele é não convexo ou também chamado de côncavo.
Observe o polígono a seguir.
Ele é considerado convexo pois o segmento de reta [A,B], independentemente para onde for movido, mantendo os pontos A e B dentro do polígono, possuirá todos os pontos do segmento também dentro do espaço.
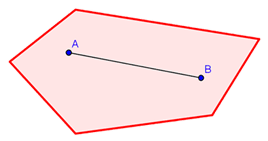
Imagem: Reprodução/matematica.pt
Agora, observe o polígono abaixo.
Ele não é convexo, pois o segmento de reta [C,D], mesmo com as extremidades dentro do polígono, tem pontos que estão fora dele.
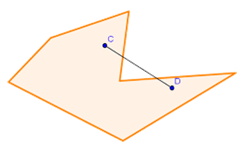
Imagem: Reprodução/matematica.pt
Os polígonos convexos possuem os seguintes elementos:
Os polígonos convexos possuem as seguintes propriedades:
d = n(n – 3)/2
Sendo d o número de diagonais do polígono e n o seu número de lados.
S = (n – 2)180
Sendo S a soma dos ângulos internos do polígono e n é o número de lados que ele possui.
Falamos dos polígonos convexos e não convexos, mas agora vamos falar um pouquinho sobre os regulares.
Quando um polígono apresenta todos os lados e ângulos congruentes, ou seja, possuem a mesma medida de lados e ângulos, sendo equiláteros e equiângulos, são considerados polígonos regulares.
Hora de praticar! Confira algumas questões de edições anteriores do Enem que abordam a temática dos polígonos. Resolva cada um dos exercícios para treinar.
As questões foram retiradas do banco de provas e gabaritos do Inep.
O Atomium, representado na imagem, é um dos principais pontos turísticos de Bruxelas. Ele foi construído em 1958 para a primeira grande exposição mundial depois da Segunda Guerra Mundial, a Feira Mundial de Bruxelas.
Trata-se de uma estrutura metálica construída no formato de um cubo. Essa estrutura está apoiada por um dos vértices sobre uma base paralela ao plano do solo, e a diagonal do cubo, contendo esse vértice, é ortogonal ao plano da base. Centradas nos vértices desse cubo, foram construídas oito esferas metálicas, e uma outra esfera foi construída centrada no ponto de interseção das diagonais do cubo. As oito esferas sobre os vértices são interligadas segundo suas arestas, e a esfera central se conecta a elas pelas diagonais do cubo.
Todas essas interligações são feitas por tubos cilíndricos que possuem escadas em seu interior, permitindo o deslocamento de pessoas pela parte interna da estrutura. Na diagonal ortogonal à base, o deslocamento é feito por um elevador, que permite o deslocamento entre as esferas da base e a esfera do ponto mais alto, passando pela esfera central.
Considere um visitante que se deslocou pelo interior do Atomium sempre em linha reta e seguindo o menor trajeto entre dois vértices, passando por todas as arestas e todas as diagonais do cubo.
 Disponível em: http://trupedatrip.com. Acesso em: 25 out. 2019.
Disponível em: http://trupedatrip.com. Acesso em: 25 out. 2019.
A projeção ortogonal sobre o plano do solo do trajeto percorrido por esse visitante é representada por
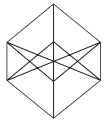
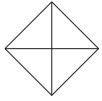
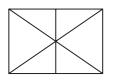

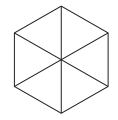
O dono de uma loja pretende usar cartões imantados para a divulgação de sua loja. A empresa que fornecerá o serviço lhe informa que o custo de fabricação do cartão é de R$ 0,01 por centímetro quadrado e que disponibiliza modelos tendo como faces úteis para impressão:
O dono da loja está disposto a pagar, no máximo, R$ 0,80 por cartão. Ele escolherá, dentro desse limite de preço, o modelo que tiver maior área de impressão.
Use 3 como aproximação para π e use 1,7 como aproximação para √3.
Nessas condições, o modelo que deverá ser escolhido tem como face útil para impressão um
Muitos brinquedos que frequentemente são encontrados em praças e parques públicos apresentam formatos de figuras geométricas bidimensionais e tridimensionais. Uma empresa foi contratada para desenvolver uma nova forma de brinquedo. A proposta apresentada pela empresa foi de uma estrutura formada apenas por hastes metálicas, conectadas umas às outras, como apresentado na figura. As hastes de mesma tonalidade e espessura são congruentes.
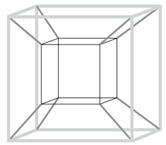
Com base na proposta apresentada, quantas figuras geométricas planas de cada tipo são formadas pela união das hastes?
Uma empresa produz painéis solares de energia elétrica, com a forma de retângulo, que geram 5 MWh (megawatts-hora) por metro quadrado. Cada painel tem 3 m de largura e 6 m de comprimento. O selo verde de eficiência é obtido se cada painel solar gerar, no mínimo, 150 MWh de energia solar. Para obter o selo verde, a empresa decide alterar apenas a largura dos seus painéis solares.
O número mínimo, em metro, que a empresa deve aumentar na largura dos seus painéis solares é
Um suporte será instalado no box de um banheiro para serem colocados recipientes de xampu, condicionador e sabonete líquido, sendo que o recipiente de cada produto tem a forma de um cilindro circular reto de medida do raio igual a 3 cm. Para maior conforto no interior do box, a proprietária do apartamento decidiu comprar o suporte que tiver a base de menor área, desde que a base de cada recipiente ficasse inteiramente sobre o suporte. Nas figuras, vemos as bases desses suportes, nas quais todas as medidas indicadas estão em centímetro.
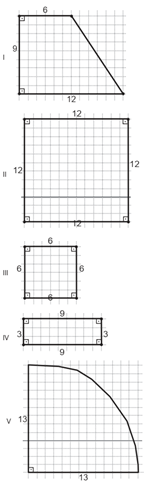
Utilize 3,14 como aproximação para π. Para atender à sua decisão, qual tipo de suporte a proprietária comprou?
Depois de treinar com os exercícios acima, uma dica é continuar com uma rotina de resolução de questões.
Você pode utilizar as questões de provas do Enem anteriores, que estão disponíveis no site do Inep.
Também tem como conferir o programa de provas com os assuntos com maior tendência a cair na prova de Matemática e suas tecnologias, fazendo uma espécie de checklist do Enem.
Não deixe de seguir esses passos para ficar afiado no assunto e tirar uma boa nota no Exame! Boa sorte!
Por Redação Blog do EAD
Gostou deste conteúdo? Compartilhe com seus amigos!

2025 © BLOG DO EAD | Todos os Direitos Reservados
Explore carreiras, mercado de trabalho e cursos de graduação no Blog do EAD. Descubra oportunidades de aprendizado e dicas para seu desenvolvimento pessoal e profissional.
2024 © BLOG DO EAD | Todos os Direitos Reservados